Espiral Aurea

El número de oro, Φ (FI), también conocido como la proporción áurea. Es uno de los conceptos matemáticos que aparecen una y otra vez ligados a la naturaleza y el arte, compitiendo con PI en popularidad y aplicaciones. Φ Esta ligado al denominado rectángulo de oro y a la sucesión de Fibonacci. Aparece repetidamente en el estudio del crecimiento de las plantas, las piñas, la distribución de las hojas en un tallo, la formación de caracolas... y por supuesto en cualquier estudio armónico del arte.

El valor numérico de Φ es de 1,618... . Φ.


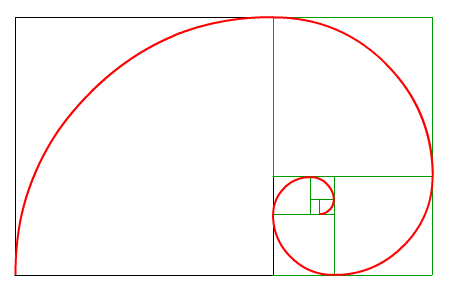
La espiral aurea es la curva compuesta por una sucesión de cuartos de circunferencia tangentes a cuadrados cuyos lados están en razón áurea.

La construcción es muy sencilla:

Dibujamos un rectángulo áureo según el método explicado antes. Lo tendremos pues descompuesto en un cuadrado y otro rectángulo más pequeño (que sabemos que es a su vez áureo).
En el cuadrado dibujamos circunscrito un cuarto de circunferencia.
Dividimos el segundo rectángulo áureo en un cuadrado y un rectángulo (basta llevar con el compás el lado más estrecho del triángulo sobre el mayor para tener la longitud del lado del cuadrado).
En el nuevo cuadrado dibujamos circunscrito un cuarto de circunferencia de modo que empiece donde terminó el trozo de circunferencia del punto 2.
Se repite el proceso indefinidamente.